前回のエントリーで、フランスの最も美しい村データベースサイトにて「データ分析もフル活用したおすすめルート作成シミュレーション機能」ができるといいなと思いつきで書いたのですが、意外と実現可能性が高いような気がしてきました。
先日、最近仕事でよく使っているRという統計解析ソフトを利用した最適化計算についていろいろ調べていたところ、偶然「巡回セールスマン問題」というものに遭遇。
What is the “Travelling Salesman Problem (TSP)”, excerpted from Wikipedia
The traveling salesman problem (TSP) is a combinatorial optimization problem in which, given a set of cities and a travel cost (e.g., distance) between each two cities, the salesman must find the minimum total travel cost for a route that travels through all the cities exactly once and returns to the starting point. (It is a combinatorial optimization problem to find the shortest path for a salesman who travels to several cities only once. (Source: Wikipedia)
I’ve been thinking about it for a while. I happened to be reading an R manual, and in the optimization section, there was an example of this traveling salesman problem algorithm.
It seems to be a very famous problem in computer science and algorithm science. I am ashamed to say that I did not know about it at all.
At that time, it occurred to me that maybe this could be used to create the best route for visiting beautiful villages.
Again from Wikipedia.
This problem belongs to a class of problems called NP-hard in computational complexity theory. (Source: Wikipedia)
I heard that you’re a good friend of mine.
NP-hard problems are considered to have no polynomial-time algorithm for arbitrary problem examples of arbitrary size, and in the case of the traveling salesman problem, for relatively small problem examples of no more than about 2000 cities, or even for some problem examples, if it is acceptable that no solution can be obtained In the case of the traveling salesman problem, the branch-and-bound method (which combines linear programming and logic trees) or the resection plane method (which combines linear programming and cyclic groups) can often provide an exact solution in about a day or less on a personal computer. (Source: Wikipedia)
This also seems to be the case.
Indeed, I was able to find plenty of libraries and sample code in R, Python, and other languages on the net to solve this problem.
It also occurred to me that this could be applied to the “Tour of Italy’s Most Beautiful Villages” that we’ll be doing next week.
So, let’s get started. First we tried R, but the sample code we found on the net didn’t work, so we switched to Python. Download and use the solver here.
図形描写などしなければ、基本的には、“src/greedy_tsp.py”にある”solve_tsp_numpy”という関数のみでOK。必要な外部モジュールもnumpyだけでOK。

手元で用意するデータは、都市間距離行列のみ。(後述しますが僕はGoogle Direction APIを利用して移動時間行列を自作しました。)
とりあえず出来上がったのは、こちら。
I’ve written down a rough recipe for making it.
- イタリアの最も美しい村リスト、座標データを用意(サルディーニャ島除く南イタリア48箇所)
- Pythonを適当に書いて、GoogleのDirection APIより2つの村の移動距離、移動時間を取得(JSONファイル)
- 上記で取得した移動時間を並び替えて行列を作る(numPyを適宜利用)
- solve_tsp_numpyに上記行列を入れて、TSP solver実行
- 上記solverで求めた最適順リストに従って村リストを並び替えJSON形式でエクスポート(Pythonはここまで)
- 簡単なhtmlファイルを作成、上記JSONファイルを読み込み、Google Maps APIを利用、訪問対象の村を最適ルート順に番号をつけてマーカー表示
- 最適ルート順に村々を直線で結ぶ(Polylineを利用)
(If I have time, I’ll write about how to make it more carefully next time.
This is way better than I expected! If you look closely, you can see that it’s a route that you wouldn’t have thought of based on genus decisions.
In particular, where the straight lines cross, such as the 4th to 7th in Sicily, or the 37th to 41st in the eastern heel. It’s no wonder that it’s difficult to make a decision without mechanical means.
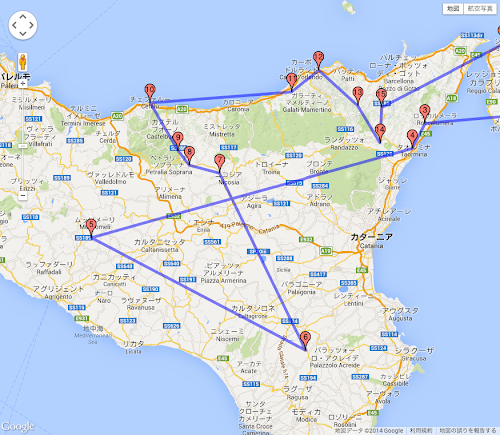
The starting point of this trip is not the village “1” on this map, but you can start from any number on the way.
There are 230 of the most beautiful villages in Italy, and 48 of them are in the south of Italy, which we will visit this time, so there is no better way than to visit them as efficiently as possible.
There are still a lot of improvements to be made (using actual routes instead of straight lines between villages, making it so that calculations can be done on the web server, etc.), but I bet this alone will help a lot on this trip!
By the way, Google Map is too convenient and amazing.


